SUDOKU

Sudoku : Unité à six espions

La notion de Rectangle unique (RU), qui sous-tend toutes les techniques d’unicité que nous avons étudiées jusqu’ici, peut-être étendue à des structures plus grandes que les simples rectangles de quatre cases. Ainsi nous allons voir quelques cas d’unicité sur six cases. Nous appellerons ce nouveau rectangle, le Rectangle Élargi (RÉ).
Nous avons divisé ces RÉ en deux catégories :
6 espions et 6 espions V1 et chacune d’elle se déclinant en trois variantes.

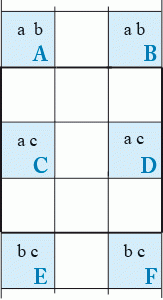
Modèle à solution multiple :
Examinons ce schéma, nous avons six candidats répartis sur trois zones sudoku. On a un cas de solutions multiples.
En effet on peut avoir en particulier comme solutions :

Étudions quelques cas d’unicité :
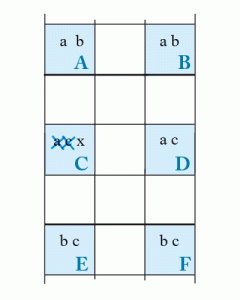
6 espions
Pour éviter une solution multiple, il faut qu’au moins une des cases A , B , C , D , E ou F contienne un candidat supplémentaire qui sera immédiatement validé.
C’est le cas dans ce schéma.
Le candidat x de la case C doit être validé pour éviter une solution multiple.
Ce qui permet de supprimer les candidats aet c de la case C .

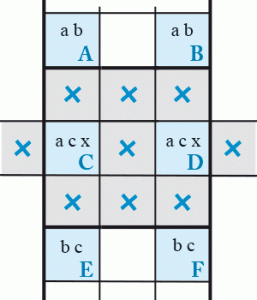
6 espions + 1
Voici la première variante de la Danse des 6 espions. Ici deux cases contiennent un candidat supplémentaire qui est le même dans les deux cases. On va donc pouvoir éliminer tous les candidats des cases qui voient les deux cases ayant ces candidats supplémentaires.
C’est la Danse des 6 espions + 1.
Dans le schéma présenté, toutes les cases du bloc contenant les deux candidats supplémentaires du Rectangle Élargi, ne peuvent pas contenir le candidat x, de même que toutes les cases de la ligne (ou la colonne dans le cas d’un Rectangle Élargi horizontal) qui contient les cases C et D . Ce sont les cases grises.

6 espions + 2
Voici la deuxième variante de la Danse des six espions. Ici, il y a deux candidats supplémentaires différents dans deux cases du Rectangle Élargi ayant une zone sudoku commune. On va donc pouvoir éliminer des candidats dans la mesure où ces deux candidats supplémentaires formeront un ensemble figé avec au moins une autre case de la même zone sudoku contenant ces deux candidats.
C’est la Danse des six espions + 2.
Dans le schéma ci-contre, les cases C et D du Rectangle Élargi ont chacune un candidat supplémentaire différent. Pour éviter une solution multiple, l’un des deux candidats sera validé. La case G , contenant les deux candidats supplémentaires, va nous permettre d’effectuer les éliminations de tous les candidats x et y des cases en gris appartenant aux mêmes zones sudoku que les cases C , G et D.

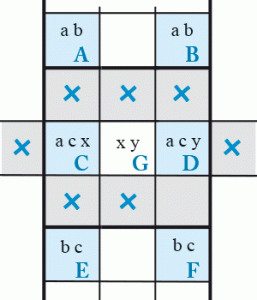
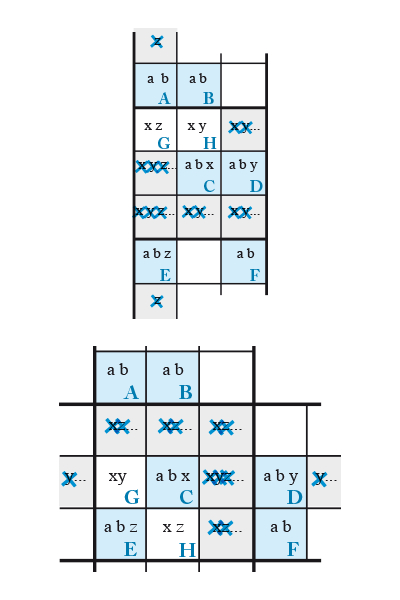
6 espions + 3
Voici la troisième variante de la Danse des six espions. Nous avons maintenant trois candidats supplémentaires différents répartis d’une manière aléatoire dans certaines des six cases du Rectangle Élargi. Il faudra donc trouver au moins deux Cases ajoutées pour figer ces ensembles de candidats et ainsi procéder à quelques éliminations. C’est une variante qui demande beaucoup d’attention, car les combinaisons sont assez nombreuses et dépendent de la disposition non seulement des candidats supplémentaires dans le Rectangle Élargi, mais aussi de la position des Cases ajoutées.
Le schéma ci-contre présente un cas de figure simple et logique. Il y a trois candidats supplémentaires, x, y et z, répartis dans trois cases distinctes du Rectangle Élargi, C , D et E. On a deux Cases ajoutées, G et H , qui contiennent respectivement xz et xy, choisies de telle manière que quelle que soit la combinaison finale de ces deux (parfois plus) cases, le Rectangle Élargi contienne au moins un candidat supplémentaire qui empêchera les solutions multiples.

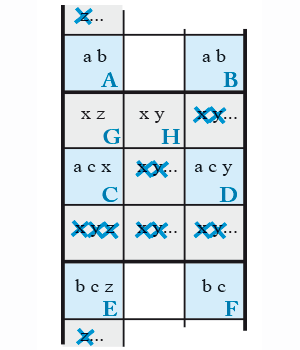
6 espions V1
La Danse des six espions peut s’appliquer d’une manière légèrement différente, ce qui va générer la version V1 de la technique. Jusqu’à présent, nous avions pour composer le Rectangle Élargi, trois candidats différents regroupés par deux et alignés en colonne et en ligne. Maintenant, nous n’avons que deux candidats différents placés dans six cases de trois zones sudoku distinctes et chaque couple voit un autre couple deux fois seulement. Cela peut donner plusieurs cas de figure.
Voici deux configurations pour lesquelles on a dessiné la solution multiple que l’on n’autorise pas et une solution unique avec un candidat x dans l’une des six cases du Rectangle Élargi qui sera validé pour sortir de cette situation.

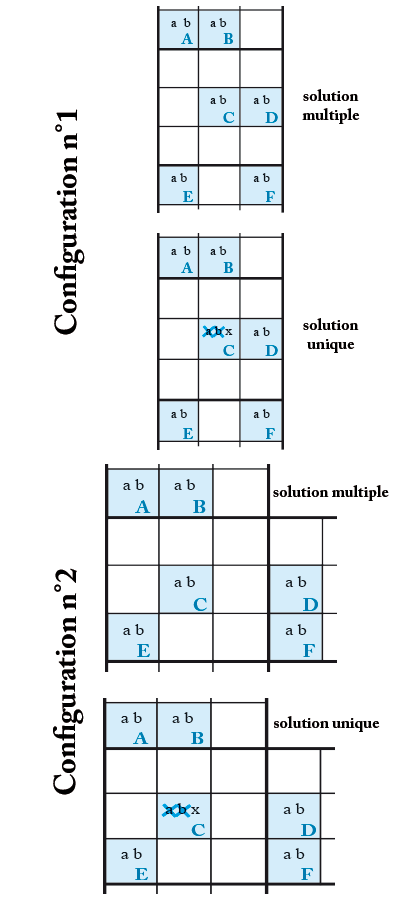
6 espions V1 + 1
On trouve dans la série la Danse des six espions V1 trois variantes qui correspondent à la présence de candidats supplémentaires dans les cases du Rectangle Élargi. Ici, nous avons les Six espions V1 + 1, avec au moins deux candidats supplémentaires identiques dans le Rectangle Élargi.
Les éliminations possibles dépendent de la position des deux candidats supplémentaires et de la configuration des cases du Rectangle Élargi. D’une manière générale, toute case qui voit les deux candidats supplémentaires ne pourra pas contenir ce candidat.
Ainsi dans le schéma du haut, dans la colonne contenant les cases du Rectangle Élargi à candidats supplémentaires, tous les candidats x des cases grisées devront être supprimés.
Dans le schéma ci-dessous, aucune des cases grises ne pourra contenir le candidat x, car les deux occurrences du candidat supplémentaire sont dans le bloc central.

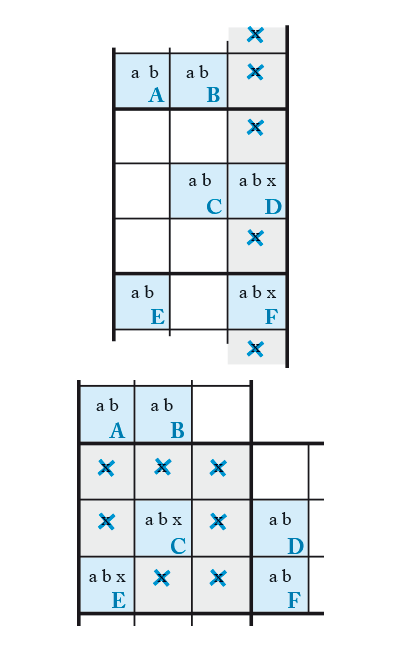
6 espions V1 + 2
Voici maintenant la deuxième variante de l’Unicité à Six espions V1 : la Danse des six espions V1 + 2. Comme dans la variante précédente, nous avons deux candidats supplémentaires dans deux cases du Rectangle Élargi. Mais dans cette version, ces deux candidats sont différents. Il faudra donc utiliser une Case ajoutée pour figer l’ensemble et ainsi procéder à des éliminations de candidats. Celles-ci dépendent bien sûr de la configuration des Six espions et de la disposition des candidats supplémentaires dans le Rectangle Élargi. Dans le schéma ci-contre, les candidats supplémentaires du Rectangle Élargi, x et y, se trouvent dans les cases C et D. On adjoint à cet ensemble une Case ajoutée G qui elle aussi contient les candidats x et y. Ainsi, l’un au moins des candidats x et y du Rectangle Élargi doit être validé pour que la grille n’ait qu’une solution et donc tous les autres candidats xy du bloc doivent être supprimés. Dans l’exemple ci-dessous, on part sur le même raisonnement, mais les candidats supplémentaires du Rectangle Élargi et la case G sont disposés de telle manière que seuls les candidats x du bloc seront supprimés alors que sur la ligne CD, x et y seront supprimés.

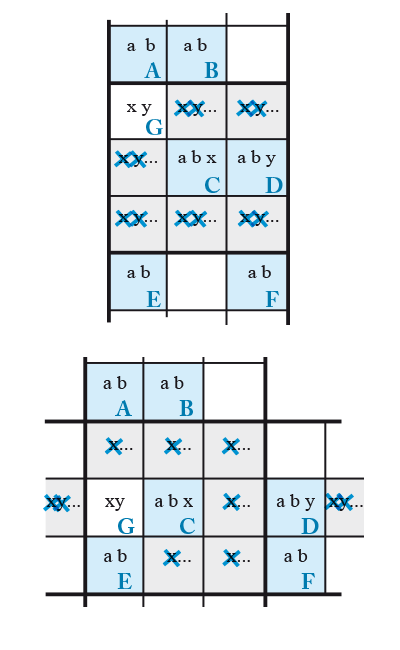
6 espions V1 + 3
La Danse des six espions V1 + 3, vous l’aurez sans doute deviné, comporte un Rectangle Élargi (RÉ) avec trois candidats supplémentaires parmi ses cases. Il faudra donc faire appel encore une fois à des Cases ajoutées pour figer ces candidats supplémentaires et ainsi pouvoir effectuer des suppressions de candidats.

Examinons deux cas théoriques.
Dans le premier schéma, les cases C , D et E du RÉ contiennent des candidats supplémentaires, x, y et z. Nous prenons comme Cases ajoutées  G et H . Aucune case de la colonne comportant AGE ne peut contenir le candidat z car sinon G = x et H = y et tous les candidats supplémentaires du RÉ disparaissent. De même, dans le bloc, aucune des cases grises ne peut contenir les candidats x ni y.
De même, dans le schéma du dessous, la ligne comportant GCD ne peut contenir le candidat y et le bloc central, les candidats x ni z. Prenons une case du bloc : si elle est égale à x alors H = z et G = y et tous les candidats supplémentaires du RÉ disparaissent. Même chose avec le candidat z.