Technique de Sudoku
Le Rectangle maxilien
Cette technique est assez intéressante bien qu’assez rare. Cependant, elle présente l’avantage d’être facilement repérable et d’être très efficace. On la doit à M. Alfred Moscardini.
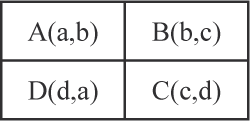
Règle :
Cette technique utilise quatre cases disposées en rectangle, A, B, C et D, qui ont chacune deux candidats :
- la case A contient les candidats a,b,
- la case B contient les candidats b,c,
- la case C contient les candidats c,d,
- la case D contient les candidats d,a.
On remarque que dans la zone Su-doku (ligne, colonne ou bloc) contenant les cases A et B, il y aura forcément le candidat b dans la case A ou dans la case B. En effet, si cela n’était pas le cas, la case A serait égale au candidat a et la case B au candidat c. Ce qui imposerait aux cases C et D d’avoir un candidat identique, le d : c’est impossible.
On raisonne de la même manière pour les zones Su-doku contenant les cases B et C, puis les zones contenant les cases C et D, et enfin les zones contenant les cases D et A.
Ainsi, par sa disposition en rectangle, on a un ensemble très puissant que l’on peut considérer uni par des liens forts.
En terme d’élimination de candidats, on pourra donc supprimer tous les candidats :
- b qui se trouvent dans la zone Su-doku contenant les cases AB,
- c qui se trouvent dans la zone Su-doku contenant les cases BC,
- d qui se trouvent dans la zone Su-doku contenant les cases CD,
- a qui se trouvent dans la zone Su-doku contenant les cases DA.
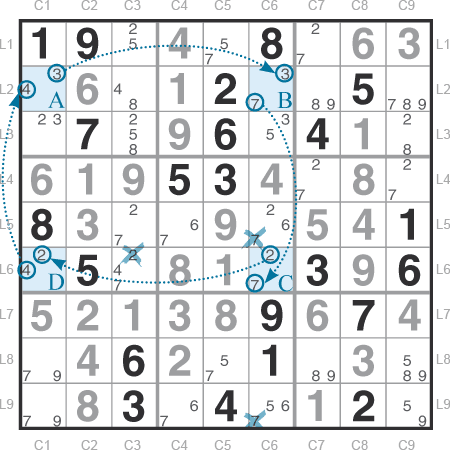
Si la case A=3, alors B=7, C=2 et D=4.
Si la case A=4, alors D=2, C=7 et B=3.
On peut donc en conclure que :
- sur la ligne CD, on aura obligatoirement un 2, soit dans la case C soit dans la case D. Tous les candidats 2 de cette ligne peuvent donc être supprimés (en L6C3).
- dans la colonne BC, on aura obligatoirement un 7, soit dans la case B soit dans la case C. Tous les candidats 7 de cette colonne peuvent être supprimés (en
