SUDOKU

Sudoku : L’Empreinte du tigre (X-Chain)

Cette méthode de résolution est très utilisée et d’une difficulté moyenne, mais sa pratique demande tout de même un peu d’expérience et surtout, de l’observation.
Avant tout, définissons une notion qui va nous être utile dans cette technique, celle de paire conjuguée : lorsqu’un chiffre candidat est possible dans deux et seulement deux cases d’une zone sudoku (c’est-à-dire une colonne, une ligne ou un bloc), alors ces deux chiffres forment une paire conjuguée.

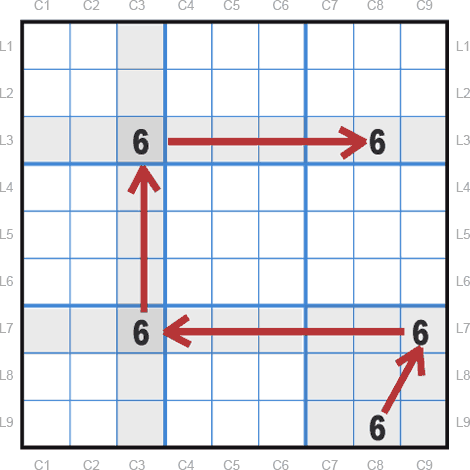
Dans la grille d’exemple ci-dessous, on ne fait apparaître que le chiffre candidat 6 afin d’illustrer notre méthode. Ici, nous avons grisé les zones Su-doku contenant des paires conjuguées. Définissons une seconde notion, celle de chaîne : c’est une série de chiffres candidats qui présentent des liens logiques entre eux. L’effet causé par un chiffre candidat sur un autre établit ce lien logique. Ici, nous allons constituer une chaîne entre les différentes paires conjuguées d’un même chiffre candidat de la grille. Ensuite, nous repérerons les deux extrémités de la chaîne. Dans notre exemple, nous les trouvons toutes deux dans la colonne 8.

Il y a une impossibilité dans cette colonne, démontrons-la :
Hypothèse : si L9C8 est vrai, L7C9 est faux, L7C3 est vrai, L3C3 est faux et L3C8 est vrai. Donc les deux extrémités de la chaîne sont vraies. Or, une zone Su-doku ne peut pas contenir deux fois le même candidat : on a bien une impossibilité dans la colonne 8.

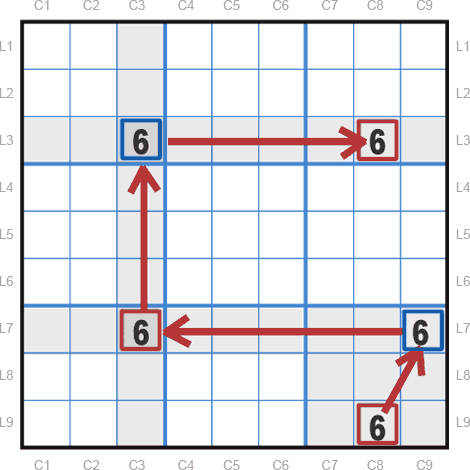
Illustrons cette impossibilité par des couleurs.
Dans chaque zone sudoku, colorions de deux couleurs différentes chaque chiffre candidat d’une paire conjuguée : dans la chaîne, on obtient une alternance des couleurs. Or, on voit clairement maintenant que dans la colonne 8, les chiffres candidats situés aux extrémités de la chaîne sont de couleur identique. Il faut en déduire que les candidats rouges ne sont pas les bons candidats et que les cases bleues contiendront le candidat 6.

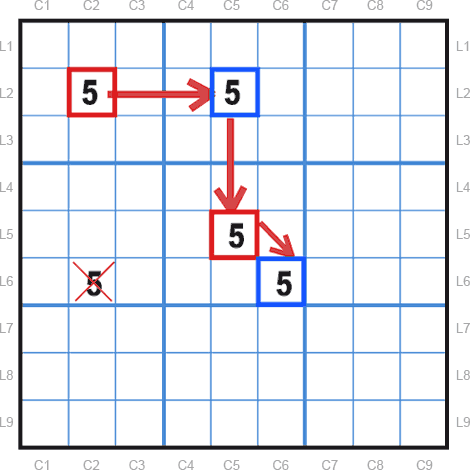
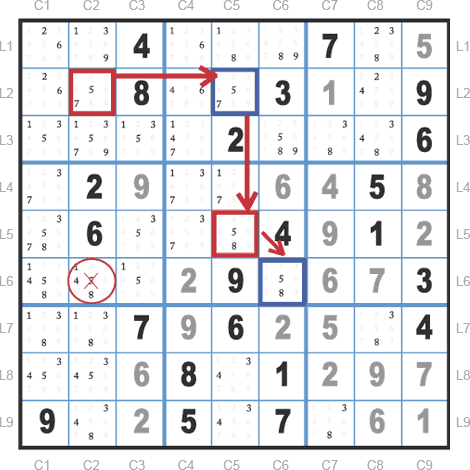
Cependant, il est rare d’observer une chaîne aussi visible, évidente. En voici donc une variante.
Sur la chaîne de l’exemple ci-dessous, si l’une des extrémités est vraie, l’autre sera fausse et inversement.
Le candidat 5 en L6C2 est à l’intersection des extrémités de la chaîne.
Si l’extrémité L2C2 est vraie, le candidat L6C2 sera faux.
Si, à l’inverse l’extrémité L6C6 est vraie, le candidat L6C2 sera faux également.
Dans tous les cas de figure, le candidat situé à l’intersection des extrémités de la chaîne peut être exclu.