SUDOKU

Sudoku : Histoire d’un secret révélé (ou la recherche d’un doublon ou triplet)

Cette cinquième technique de base de résolution d’une grille de sudoku est surnomée l’histoire d’un secret révélé. Cette figure est plus compliquée que les précédentes mais elle représente une étape utile avant d’accéder aux techniques de jeu qui nécessitent de positionner les chiffres candidats. Pour ce faire, on va, essayer de positionner un doublon ou un triplet de chiffres candidats dans une zone sudoku (ligne, colonne ou bloc), ce qui permettra de valider ou d’invalider d’autres chiffres candidats.

Découvrez trois exemples d’application de cette technique du secret révélé :

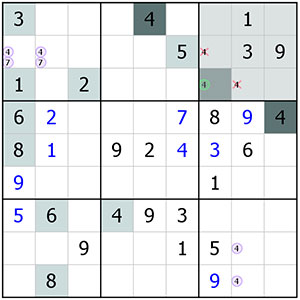
Voici un premier exemple, on considère le bloc 7 et son intersection avec la ligne 8. On remarque que les candidats 3, 6 et 8 qui appartiennent à la ligne ne sont pas dans le bloc. Cela nous permet de poser virtuellement ces 3 candidats dans les cases L7C3 et L8C12. Ce triplet posé nous impose pour compléter le bloc de positionner dans les cases L8C12, les candidats 2 et 9 et par le 9 en L5C1, de valider L8C1 = 5 et L8C2 = 9.

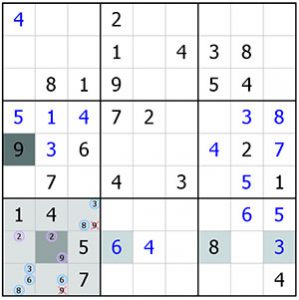
Voici un deuxième exemple, on s’intéresse à la ligne 1 et à l’intersection du bloc 2 avec la colonne 5. Les chiffres 2 et 8 de cette colonne, nous donne le doublon 2, 8 en L1C46. Si l’on considère maintenant le ligne 1, on peut affirmer grâce au 4 de la case L4C7 que L1C1 = 4.

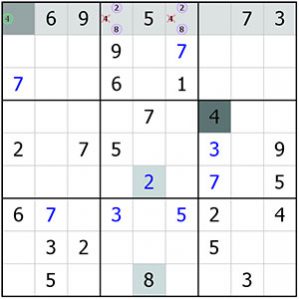
Voici un troisième cas de figure qui est un peu plus complexe. Dans un premier temps, considérons le bloc 9 et positionnons virtuellement les candidats 4 en L89C8. On regarde maintenant le bloc 1. Les chiffres 6 et 8 des colonnes 1 et 2 nous permettent de positionner ces chiffres en tant que candidats dans les cases L12C3. Les chiffres 5 et 9 de la ligne 2 seront mis en tant que candidats dans les cases L13C2. Ce qui nous permet de mettre les candidats 4 et 7 dans les cases L2C12. L’ensemble des candidats 4 réels ou virtuels étant projetés sur le bloc 3 donne L3C7 = 4.