SUDOKU
TECHNIQUES DE SUDOKUSudoku : L’Approche du tigre (AIC)
La méthode sudoku de l’approche du tigre se présente comme une généralisation de toutes les techniques dites « du tigre » que nous avons étudiées précédemment : la Griffe, l’Empreinte et la Piste.
Rappelons ce qu’est une inférence (voir dans la Piste du tigre) : c’est une opération logique portant sur des propositions tenues pour vraies qu’on appelle aussi prémisses. Un exemple concret connu : en rentrant chez moi, je vois une ambulance devant ma maison (ce fait est réel = prémisse). Je ne peux pas m’empêcher d’imaginer que quelqu’un est malade à la maison (je formule une inférence). Formuler ou envisager une inférence, c’est imaginer une ou des conclusions à partir d’un fait établi.
Nouvelles définitions
Dans cette méthode sudoku de l’approche du tigre, il existe trois types de liens possibles :
– le duo de lieu (ou bi-location) : c’est le lien qui existe entre deux cases si elles appartiennent à la même zone Su-doku (ligne, colonne ou bloc) et si elles partagent un même chiffre candidat. C’est un lien que nous avons très souvent rencontré en pratiquant les techniques dites « du tigre ».
– le duo de valeur (ou bi-value) : dans une case qui contient seulement deux candidats, c’est le lien qui existe entre ces deux candidats.
– le duo d’ensemble (ou ALS in chains) : cette notion complexe utilise la notion d’ensemble presque figé (ALS), comme dans la technique de l’Attaque du cobra.
Rappels
1 – Quand un lien existe entre deux candidats, on peut formuler une inférence et déterminer la valeur de l’un des deux : dans le cas d’un duo de lieu, si une case contient le candidat A, alors la seconde case du lien ne peut pas le contenir et vice versa. On parle alors d’une inférence faible. À l’inverse, si l’une des cases du lien ne contient pas le candidat A, alors la seconde doit le contenir. On parle d’une inférence forte.
Toutefois, il est important de souligner qu’une inférence forte est d’abord et aussi une inférence faible.
2 – Conventions d’écriture :
– pour un lien fort, on utilise le signe (=) : L1C1=1=L1C8 indique qu’il existe un lien fort avec le candidat 1 entre les cases L1C1 et L1C8.
– pour un lien faible, on utilise le signe (–) : L1C1-1-L5C1 indique qu’il existe un lien faible avec le candidat 1 entre les cases L1C1 et L5C1.
On construit toujours une chaîne d’inférences en commençant par un lien fort, puis on alterne les liens faibles et forts jusqu’au retour au point de départ.
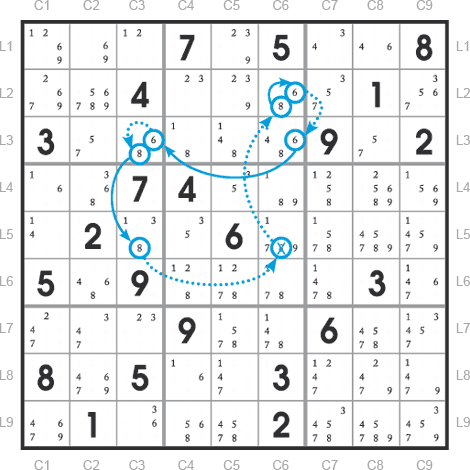
Grille de Sudoku Virtuose n°15 p.70
Dans l’exemple ci-dessus, les liens forts sont représentés par des flèches pleines et les liens faibles par des flèches en pointillé.
On remarque que les cases L2C6 et L3C3 forment deux duos de valeur à lien fort. Or, puisqu’une inférence forte est aussi une inférence faible, considérons-la comme telle. Ainsi, si le lien entre les candidats de L3C3 est faible, on va pouvoir construire une chaîne d’inférences alternées.
On peut noter cette boucle de la manière suivante :
L2C6=8=L2C6-6-L3C6=6=L3C3-8-L3C3=8=L5C3-8-L5C6-8-L2C6
Il s’agit d’une boucle d’inférences alternées irrégulières.
L’un des candidats d’inférence est le 8. La case L5C6 étant reliée par deux liens faibles, on peut supprimer le candidat 8 qui s’y trouve.
Cette déduction trouve sa justification dans la Piste du tigre ou dans l’Empreinte du tigre.
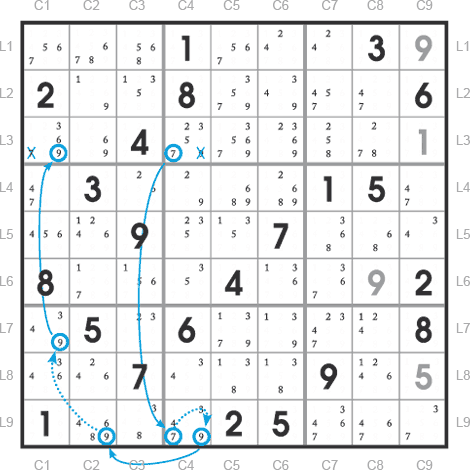
Grille de Sudoku Virtuose n°15 p.64
Ici, on laisse délibérément la chaîne ouverte.
Règle : si le début et la fin d’une chaîne d’inférences alternées se situent dans une même zone Sudoku (ligne, colonne ou bloc) et si les deux candidats de la chaîne sont différents, alors chacun de ces deux candidats peut être éliminé de l’autre extrémité de la chaîne.
Le candidat 7 de la grille ci-dessus peut donc être éliminé de la case L3C1.
Le candidat 9 de la grille ci-dessus peut donc être éliminé de la case L3C4.
Démonstration :
Si L3C4 = 7, alors L3C1 ≠ 7
Si L3C4 ≠ 7, alors L3C1 = 9 donc ≠ 7. (en suivant la chaîne bleue)
Dans tous les cas de figure, le candidat 7 ne sera jamais possible dans la case L3C1.
Une chaîne d’inférences alternées est bi-directionnelle : elle peut se lire dans les deux sens.
Si L3C1 = 9, alors L3C4 ≠ 9
Si L3C1 ≠ 9, alors L3C4 = 7 donc ≠ 9.
Dans tous les cas de figure, le candidat 9 ne sera jamais possible dans la case L3C4.
