SUDOKU

Sudoku : L’Arme et la soie (Sue de coq)

Cette manière de faire est probablement l’une des plus efficaces du monde des sudoku difficiles parce qu’elle permet, en général, de supprimer plusieurs chiffres candidats d’un seul coup, ce qui est extrêmement rare dans ce type de technique. Bien que des techniques plus modernes de résolutions (comme les chaînes forcées) permettent de s’en passer, nous tenons à maintenir cette forme pour son élégance.

On trouve cette méthode sous les noms suivants : Two-Sector Disjoint Subsets et aussi et surtout Sue de Coq, du pseudonyme de celui qui, pour la première fois, l’a mise en avant. C’était en Angleterre, à Wimbledon, en avril 2005. Il s’agit d’observer, dans une grille, l’intersection d’un bloc avec une ligne ou une colonne.

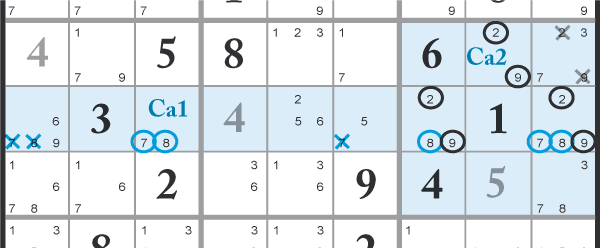
On cherche une intersection ayant deux cases et quatre candidats ou trois cases et cinq candidats. On recherche ensuite une case (que l’on va nommer Ca1) située sur la ligne (ou dans la colonne) mais à l’extérieur de l’intersection et n’ayant que deux candidats qui doivent correspondre à ceux de l’intersection. On recherche enfin une case située à l’intérieur du bloc (que l’on va nommer Ca2) et de la même manière située à l’extérieur de l’intersection et contenant les deux autres candidats de l’intersection et différents de ceux de la ligne (ou de la colonne). On pourra alors éliminer tous les autres candidats de la ligne (ou de la colonne) qui sont identiques à ceux de la case Ca1 et tous les candidats du bloc identiques à ceux de la case Ca2.