SUDOKU
TECHNIQUES DE SUDOKUSudoku : Le rectangle unique (Unique rectangle)
La technique du rectangle unique correspond à la Danse des espions inspirée de la danse des abeilles, expliquée par l’éthologue Karl von Frisch et qui lui a valu le prix Nobel de physiologie ou médecine en 1973. Du printemps à la fin de l’été, c’est la période de forte production du nectar par les fleurs, appelée miellée. Des abeilles éclaireuses ou exploratrices, souvent les plus expérimentées, partent à la recherche de la précieuse nourriture. Une fois ces zones repérées, elles retournent à la ruche délivrer leurs informations. Là, dans l’obscurité, elles vont commencer à « danser » au milieu des autres abeilles restées à la ruche. Ces danses s’effectuent dans un endroit unique de la ruche et sont très codifiées. La danse la plus simple est la danse en rond.
En termes de sudoku, aucune règle de sudoku ne stipule que les grilles doivent avoir une solution unique. Pourtant, lors de la fabrication de nos grilles, nous l’imposons comme une contrainte car nous jugeons cette règle absolument indispensable à une résolution convenable. Nous pouvons alors disposer de techniques de résolution qui se basent sur ce postulat. Ces techniques sont réunies dans une rubrique dite de la Danse des espions.
La Danse des espions se compose de quatre cases étant exactement disposées en deux lignes, deux colonnes et deux blocs.
Il est très fréquent de se tromper et d’essayer d’appliquer cette technique quand les cases du rectangle unique ne sont pas disposées convenablement. Apprenez tout de la technique Sudoku du Rectangle unique (Unique Rectangle) à partir de la méthode et d’exemples de mise en application.

Modèle à solution double :
Quatre cases placées en rectangle, contenant chacune deux candidats 7 et 8, forment une grille à deux solutions, ce qui est impossible. Il y a donc forcément un ou plusieurs autres chiffres candidats qui viennent empêcher ce cas de figure.
Les deux solutions sont :


Étudions quelques cas d’unicité :
Rectangle Unique n°1
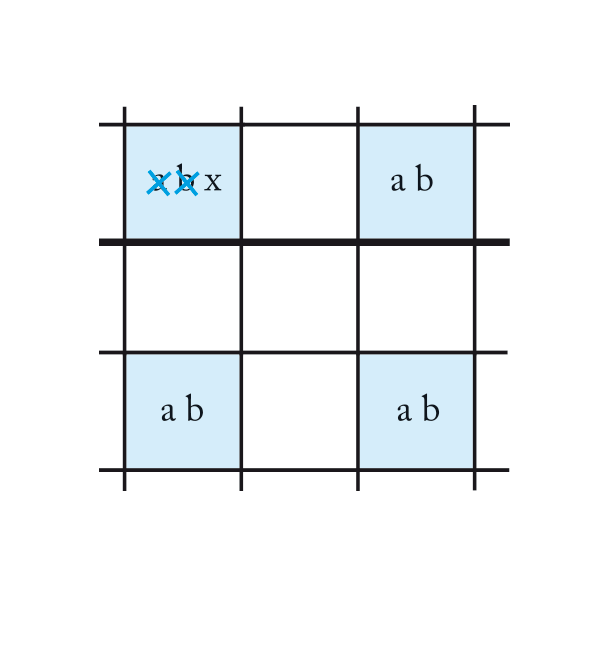
Une des cases du rectangle a un candidat supplémentaire x. Ce qui nous permet de supprimer les candidats a et b de la case abx.
C’est une des techniques avancées la plus courante et la plus facile à voir mais surtout il ne faut pas oublier que les cases du Rectangle Unique doivent être dans deux lignes, deux colonnes et deux blocs. Il est très fréquent de se tromper et d’essayer d’appliquer cette technique quand les cases du rectangle unique ne sont pas disposées convenablement.
Exemple :
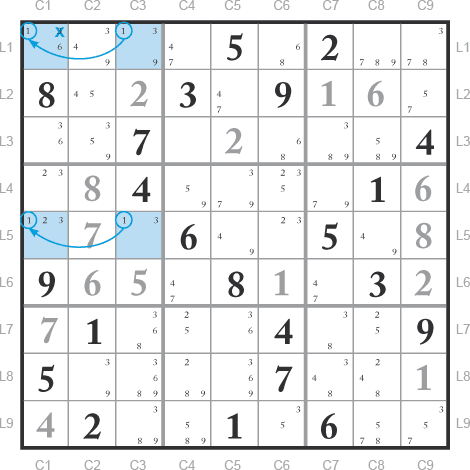
a=3 et b =5 le rectangle est indiqué par les cases en bleu et x=2.
On remarque que dans chaque bloc concerné par ce rectangle unique si l’un des candidats est 3 l’autre sera 5 et inversement. Il n’y a pas d’autre alternative sauf dans le bloc quatre qui a un candidat 2 dans une des cases du rectangle. Et pour éviter une solution double, on doit valider le 2 de la case L4C2.
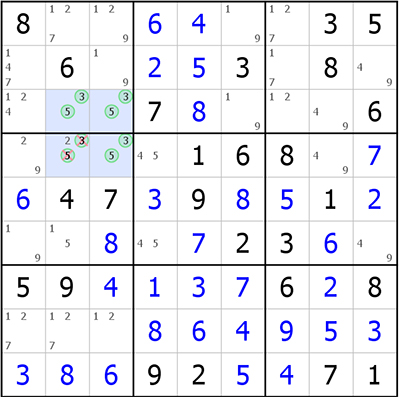
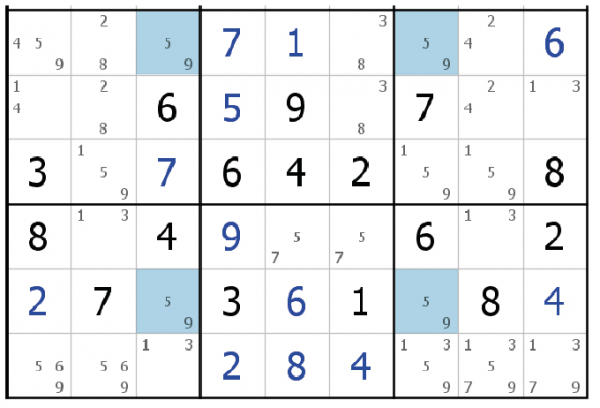
Contre-exemple : Grille de Sudoku Expert de poche n°46 p.86
On ne peut pas supprimer le 3 de la case L4C7 car le rectangle unique des candidats 5-9 appartient à quatre blocs.
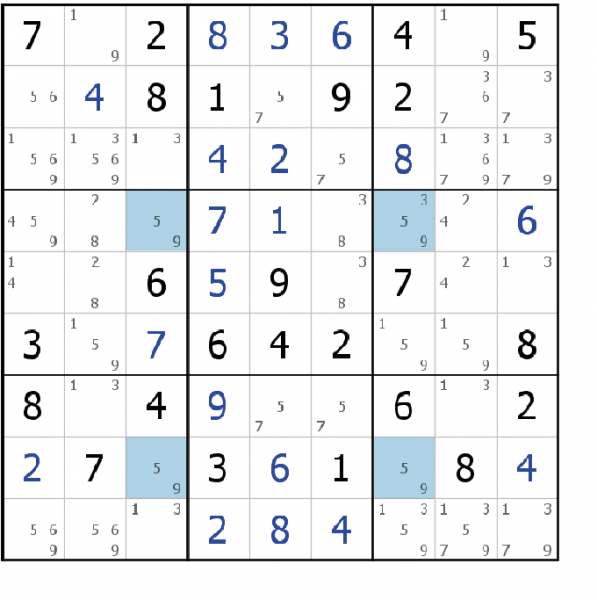
Imaginons que le candidat 3 du rectangle bleu soit absent. On a une des deux solutions mais en aucun cas les deux. Si la première case = 5, le 9 se trouvera dans le premier bloc et la solution première case = 9 n’est plus possible. Donc on ne doit pas appliquer les techniques du rectangle unique.
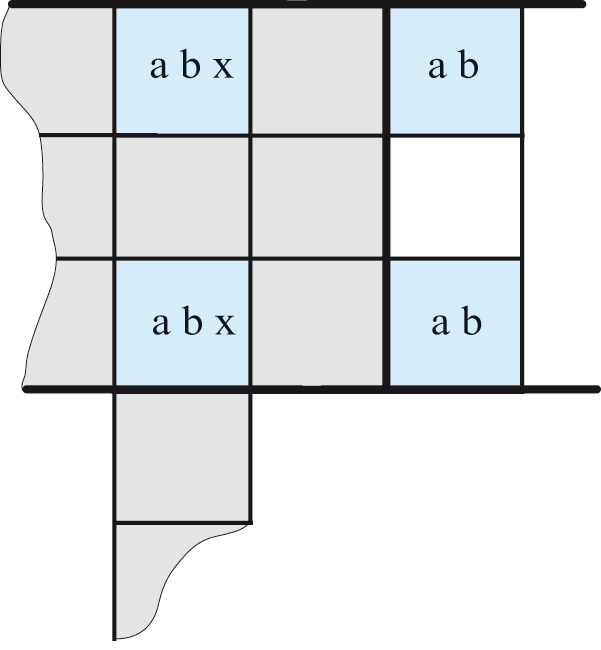
Rectangle Unique n°2
Dans cette configuration un candidat supplémentaire x est présent dans deux cases du rectangle et cela nous permet de supprimer ce candidat x de toute case voyant les deux cases du rectangle qui contiennent ce candidat supplémentaire.
Dans le schéma ci-contre tous les candidats x pourront être supprimés des cases en gris. C’est à dire la colonne et le bloc contenant les cases abx.
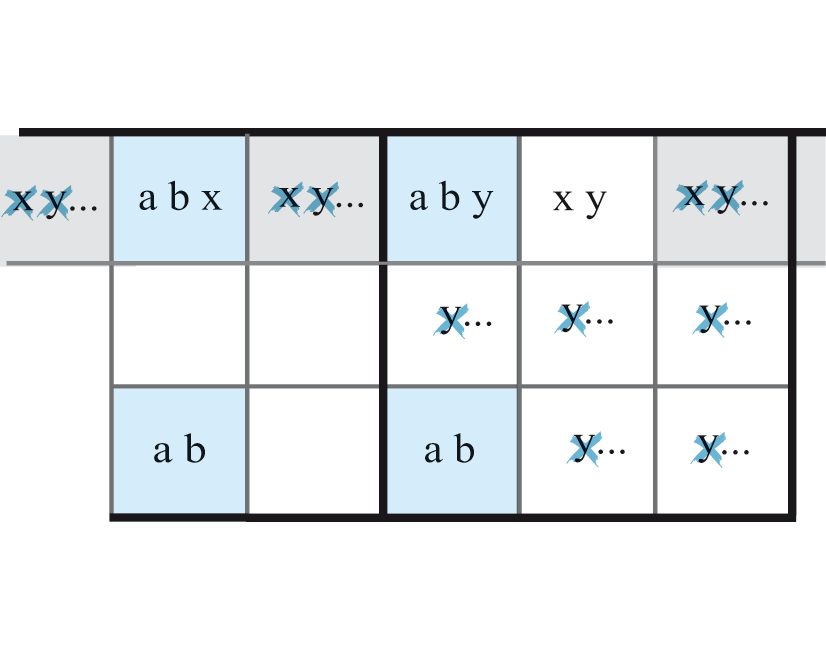
Rectangle Unique n°3-V1
On a, sur le Rectangle Unique, deux candidats supplémentaires différents x et y dans deux cases non disposés en diagonal. Combiné avec une case qui contient le couple xy, cela forme une paire cachée. Ce qui permet de supprimer toute autre occurrence de x et y dans la zone sudoku considérée (ligne, colonne ou bloc).
Rectangle Unique n°3-V2
Ce cas est plus difficile à visualiser car il n’existe pas de case à l’extérieur du Rectangle Unique contenant uniquement les candidats xy. On doit donc rechercher les cases, dans la même zone sudoku, contenant chacune un de ces candidats et aussi un candidat (ou plus) complémentaire commun à ces cases : ainsi, dans l’exemple ci-contre, le candidat complémentaire commun est le z. Dans ce cas de figure, on peut supprimer des cases grises tous les candidats x, y mais aussi le candidat z.
Rectangle Unique n°4
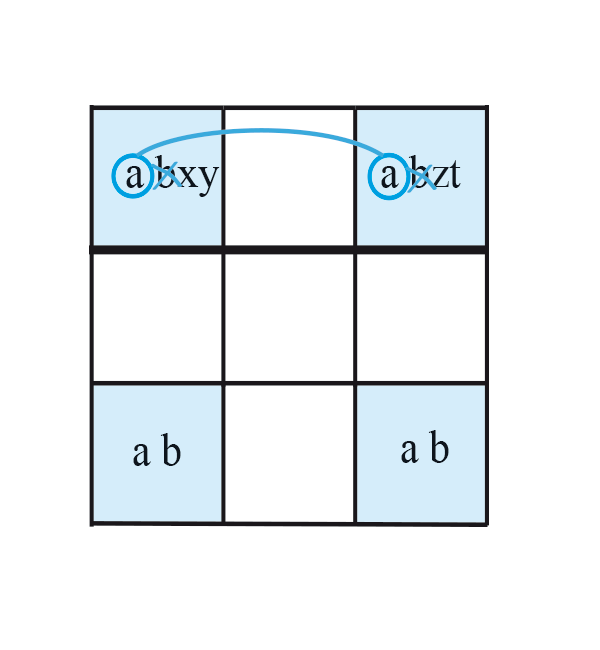
Voici une autre variante assez facile à repérer et très efficace. On recherche un Rectangle Unique ayant des chiffres candidats en plus dans deux cases qui ne sont pas en diagonale. Mais dans cette variante, on ignore ces «extra-candidats» pour se concentrer uniquement sur les candidats du Rectangle Unique qui partagent les cases avec les extra-candidats : s’il y a un lien fort entre deux candidats du rectangle, c’est-à-dire qu’il n’existe aucune autre occurrence de a dans la zone sudoku considérée (ici la ligne), alors il sera obligatoirement dans l’une de ces deux cases et pour éviter une solution multiple à la grille, nous devons supprimer l’autre candidat du rectangle.
Rectangle Unique n°4 V1
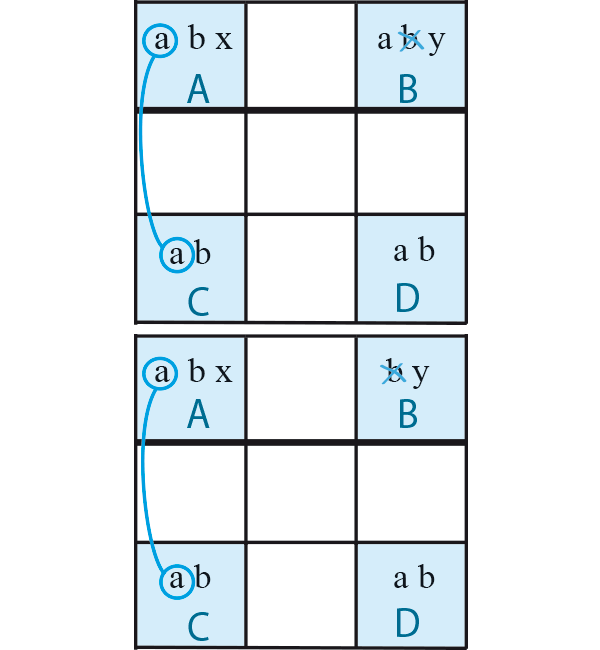
Voici une première évolution de cette technique du Rectangle Unique n°4. Nous avons toujours deux cases du rectangle qui ont des candidats supplémentaires. Nous avons toujours un lien fort qui relie deux candidats du rectangle, mais dans cette évolution, le lien se trouve entre une des cases du rectangle qui a des candidats supplémentaires et une des cases sans candidat supplémentaire. Le mode de raisonnement est assez différent des modèles précédents. Nous partons de la case D du schéma : Si D = a alors C = b et par le lien fort A = a donc la case B ne peut pas être égale à b car sinon on se retrouverait dans une situation de solution double.
Rectangle Unique n°4 V2
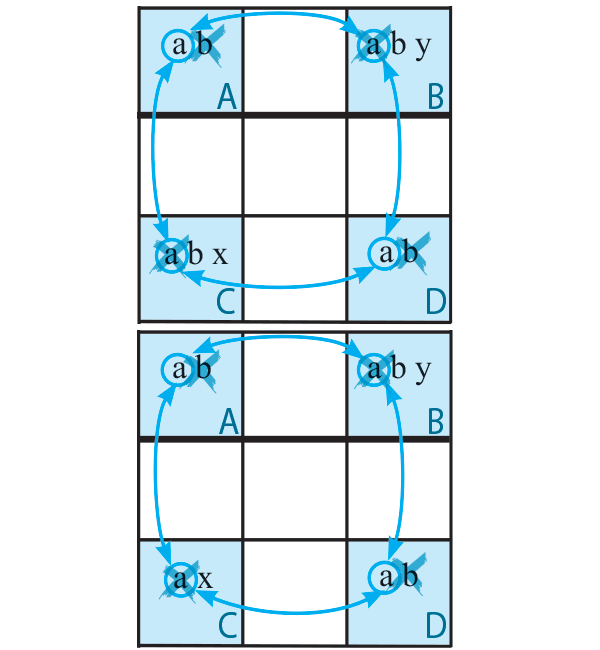
Voici une deuxième évolution de cette technique du Rectangle Unique n°4. Nous avons toujours deux cases du rectangle qui ont des candidats supplémentaires mais cette fois-ci, ces deux cases sont disposées en diagonale. On trouvera toujours un lien fort sur l’un des candidats du rectangle. Si la case B = a alors la case A = b et la case C = a par le biais du lien fort et donc la case D = b. On est dans une configuration interdite avec deux solutions possibles.Donc le candidat a doit être supprimé de la case B .
On peut se trouver dans le cas de la seconde figure, où le Rectangle Unique n’est pas complet. Il manque le candidat b de la case C. Nonobstant, le candidat a de la case B sera éliminé.
Rectangle Unique n°6
Le Rectangle Unique n°6 est une variante du n°2 mais ici, le candidat additionnel doit se trouver dans les cases en diagonale. Et donc toute case qui voit toutes les occurrences de ce candidat additionnel dans le rectangle bleu ne pourra le contenir.
Rectangle Unique n°7-2
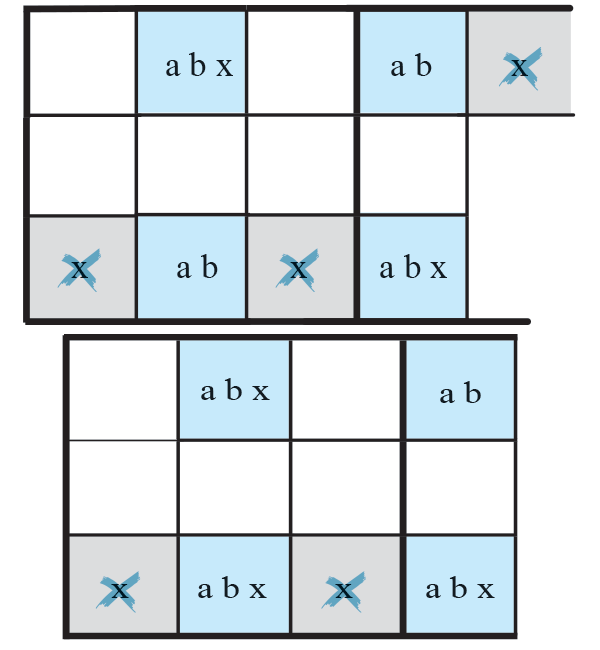
Le Rectangle Unique n°7-2 est une variante qui combine le n°3 et le n°6. Comme le n°3, on a une case à l‘extérieur du rectangle qui contient les candidats additionnels et voit ceux des cases du rectangle. Et comme le n°6, trois des cases du rectangle contiennent des candidats additionnels. Mais ces candidats additionnels sont au nombre de deux.
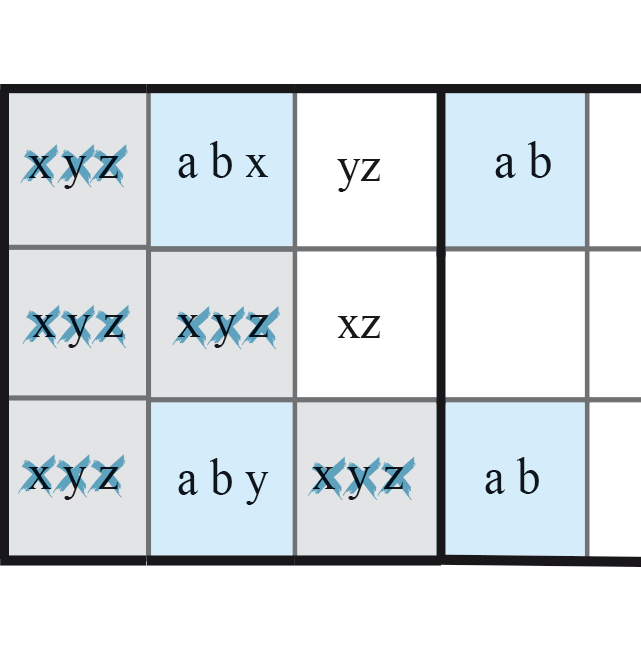
Il existe plusieurs configurations possibles de ce cas général, le jeu consistant à éviter tout cas de solution multiple. Ainsi dans le schéma ci-contre, où les candidats supplémentaires x, y sont répartis dans les cases du rectangle, les cases rose (la ligne) ne peuvent contenir x et les cases en violet (le bloc) ne peuvent contenir le candidat y. La case, cerclée de noir, qui se trouve à la fois dans le bloc et sur la ligne, ne peut, elle, contenir ni le x ni le y.
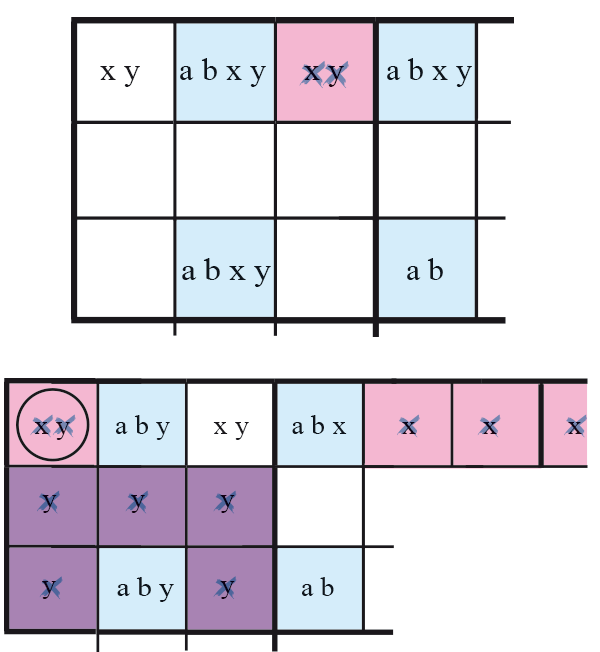
Rectangle Unique n°7-3
Le Rectangle Unique n°7-3 est une évolution logique de la version 7-2. On se trouve dans la même situation avec un Rectangle Unique ayant cette fois trois candidats supplémentaires. Ceux-ci peuvent être combinés différemment dans les trois cases du rectangle. On a de plus, non plus une, mais deux cases qui peuvent contenir ces trois candidats et uniquement ceux-ci. On a donc six cases et cinq candidats. Le jeu est d’éviter de se trouver en situation de solution multiple. Naturellement, il existe plusieurs cas d’éliminations. (H.Lemoulec en a compté 9). Plutôt que de les expliciter un à un, analysons-en un. On se trouve, dans le schéma ci-contre, avec une configuration de rectangle avec les candidats a et b dans les cases bleues. Il y a trois candidats supplémentaires, x, y et z, qui sont répartis dans trois cases du rectangle. On a de plus deux cases ne contenant que les candidats x, y et z. Si les cases roses contiennent les candidats x ou/et y, alors les cases bleues perdent tous leurs candidats supplémentaires et nous serons dans un cas interdit. Donc les cases roses ne doivent pas contenir x ou/et y. Si les cases en violet contenaient y ou/et z, on serait dans la même situation. Donc les cases en violet ne doivent pas contenir y ou/et z.