SUDOKU

Sudoku : Le Territoire du tigre (Les chaînes forcées)

Cette technique fait partie de celles qui sont assez controversées, car elles sont à la limite de la logique et de l’empirisme. Cependant nous l’avons classée dans les techniques du tigre et non dans les techniques de force brute, car elle a quand même un cohérence. Dans cette technique Sudolu du Territoire du Tigre, le terme de chaîne forcée est l’expression générique qui englobe tous les types de boucles et de chaînes qui aboutissent soit à une contradiction soit à une affirmation. On démontre ainsi qu’une case cible a un candidat qui peut être supprimé ou au contraire confirmé (il devient alors un chiffre trouvé).

Voici un exemple de suppression :
Si L5C6 = 7 alors L5C4 = 8 alors L5C4 ≠ 7.
Si L5C6 = 8 alors L6C5 = 7 alors L2C5 ≠ 7 alors L3C4 = 7 alors L5C4 ≠ 7.
Dans les deux cas de figure, la case L5C4 sera différente de 7 donc le candidat 7 de la case L5C4 peut être supprimé.

La case d’origine peut avoir deux ou trois candidats.

Voici un exemple de candidat confirmé sur une case d’origine de trois candidats :
Si L2C2 = 2 alors L5C2 = 7.
Si L2C2 = 4 alors L1C3 = 5 alors L5C3 = 2 alors L5C2 = 7.
Si L2C2 = 6 alors L1C2 = 4 alors L1C3 = 5 alors L5C3 = 2 alors L5C2 = 7.
Dans tous les cas de figure, la case L5C2 sera égale à 7, on peut donc confirmer que L5C2 = 7.

On a ici des chaînes qui ont même origine et même destination. On peut avoir aussi des chaînes qui ont des origines différentes et des destinations identiques. Elles portent alors le nom de double chaîne d’implication.

Voici un exemple de double chaîne d’implication :
Si L8C2 = 6 alors L8C6 ≠ 6 alors L5C6 = 6.
Si L4C2 = 6 alors L5C3 ≠ 6 alors L5C6 = 6.

Dans tous les cas de figure, avant de trouver les chaînes qui fonctionnent, il faut essayer plusieurs possibilités. La technique de coloriage offre une alternative à cette technique, mais on ne peut colorier qu’une fois et c’est là sa limite. Il existe des problèmes de Sudoku qui ne trouvent pas de solution par la technique du coloriage ni par les chaînes forcées du type double, mais par la combinaison des deux.

Exemple d’une grille comportant une chaîne forcée sur une case de trois candidats. Les trois cases grises sont les cibles à partir desquelles on recherche deux ou trois chaînes qui partiraient d’une même case, la case source. Dans cet exemple, c’est la case bleue L2C1 qui comporte trois candidats. Donc il faut que, quel que soit le candidat de la case source, l’on obtienne le même résultat sur les cases cibles.

Cas n°1
Si L2C1 = 2 alors L3C3 = 6 alors L1C2 = 5 alors L8C2 = 4 donc L8C4 = 8 et L7C4 = 4 et L8C9 = 3.

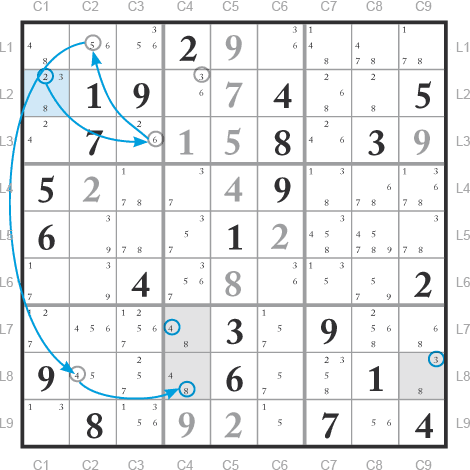
Cas n°2
Si L2C1 = 3 alors L9C1 = 1 alors L9C6 = 5 alors L9C8 = 6 alors L7C9 = 8 donc L8C9 = 3 et L8C4 = 8 et L7C4 = 4.

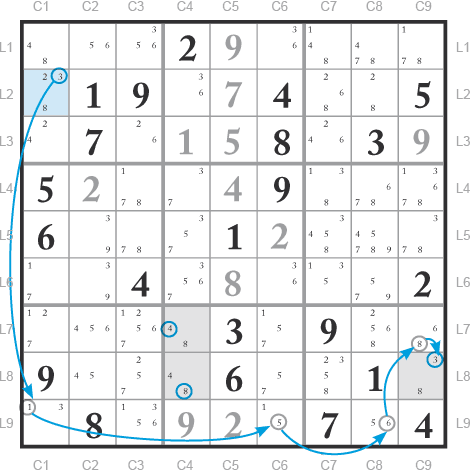
Cas n°3
Si L2C1 = 8 alors L1C1 = 4 alors L3C1 = 2 alors L3C3 = 6 alors L1C2 = 5 alors L8C2 = 4 donc L8C4 = 8 et L7C4 = 4 et L8C9 = 3.

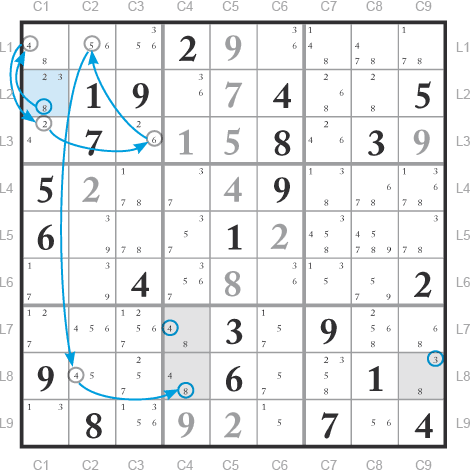
Quel que soit le candidat choisi dans la case source, on a le même résultat dans les cases cibles.
On peut donc dire que ce résultat est certain et l’on peut positionner dans L8C4 le 8 et dans L7C4 le 4 et dans L8C9 le 3.