SUDOKU

Sudoku : Les Espions LT (Uniqueness)

Nous vous présentons ici des formes assez intéressantes de la technique Sudoku des Espions cachés. C’est Alfred Moscardini qui nous a envoyé ces réflexions sur les grilles à Rectangle unique. Avant tout, rappelons qu’une grille doit avoir une solution unique et que toute situation qui pourrait aboutir à des solutions multiples doit être étudiée. Rappelons aussi que les quatre cases d’un Rectangle unique doivent se trouver dans seulement deux zones sudoku.

Unicité : principe du Rectangle unique n°1.
Cette configuration amène à supprimer les candidats a et b de la case A.

Dans tous les schémas suivants, toutes les occurrences du candidat a du bloc de droite sont représentées.
Dans les exemples ci-dessous, les «…» représentent d’autres chiffres candidats.

Unicité LT schéma 1
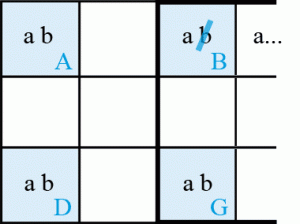
Si la case A = a, la case D = b et la case G = a car tous les candidats a du bloc sont représentés et pour des raisons d’unicité, la case B ne peut pas être égale à b qui peut donc être supprimé.

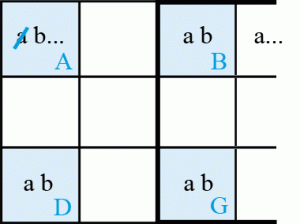
Unicité LT schéma 2
Si la case A = a, alors la case B = b et comme toutes les occurrences du candidat a du bloc de droite sont représentées, la case G = a et enfin la case D = b. Nous sommes dans un cas de solution double et pour éviter cela, la case A ≠ a.

Unicité LT schéma 3
Il n’y a que deux occurrences du candidat b dans la colonne AD. Si la case A = a, alors la case D = b et comme toutes les occurrences du candidat a du bloc de droite sont représentées, la case G = a et pour des raisons d’unicité, la case B ≠ b.

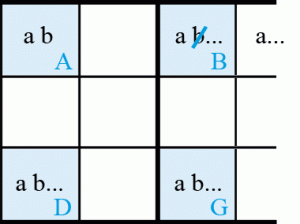
Unicité LT schéma 4
Il n’y a que deux occurrences du candidat b dans la colonne BG. Si la case A = a, comme toutes les occurrences du candidat a du bloc de droite sont représentées, la case G = a. La case D = b et la case B = b. Il y a une solution multiple donc la case A ≠ a.

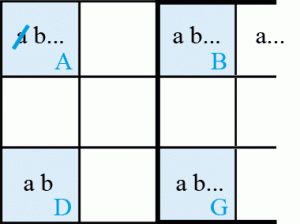
Unicité LT schéma 5
Il n’y a que deux occurrences du candidat b dans la colonne AD et sur la ligne AB. Si la case A = a, les cases B et D = b et comme toutes les occurrences du candidat a du bloc de droite sont représentées, la case G = a. Donc la case A ≠ a.

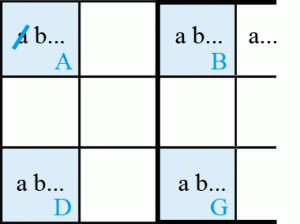
Unicité LT schéma 6
Il n’y a que deux occurrences du candidat b sur la ligne DG et que deux occurrences du candidat a dans la colonne AD et tous les candidats a du bloc de droite sont représentés.
La case B ≠ b. En effet, si B = b alors D = b, A = a et G = a, ce qui donne une solution multiple.

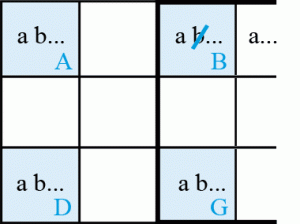
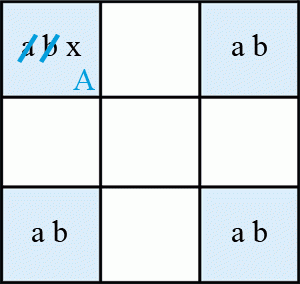
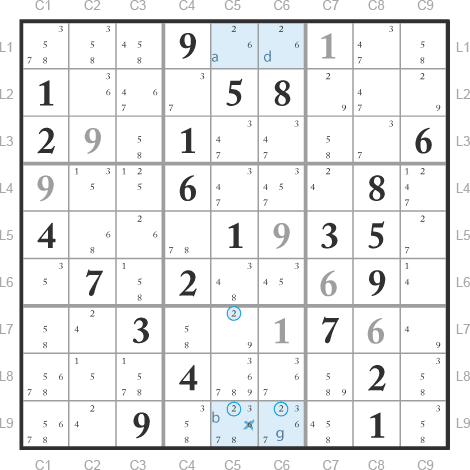
Voici un exemple de l’Unicité LT schéma 1 :
Dans le bloc 8, deux des trois occurrences du candidat 2 sont dans les cases du Rectangle unique et la troisième est dans son alignement. Si la case a, L1C5 = 2, alors L1C6 = 6 et, dans le bloc 8, il ne reste que la case g, L9C6, pour contenir le 2 et pour des raisons d’unicité la case b, L9C5, ne peut pas être égale à 6 qui peut donc être supprimé.

Voici un exemple de l’Unicité LT schéma 3 :
Il n’y a que deux occurrences du candidat 6 sur la ligne 2. Si la case a, L2C5, = 5, alors la case d, L2C4, = 6, la case g, L7C4, = 5, et donc la case b, L7C5, ne vaut pas 6 sinon nous aurions une solution double.