SUDOKU

Sudoku : POM

Inventée par Myth Jellies, cette méthode analyse les différentes manières dont les occurrences d’un même chiffre spécifique peuvent se positionner dans les cases disponibles de la grille. C’est une stratégie qu’il ne faut pas appliquer trop tôt dans la résolution de la grille sinon le nombre de possibilités est trop grand.

On trouve parfois dans la littérature sudoku cette technique sous le nom de Templating.
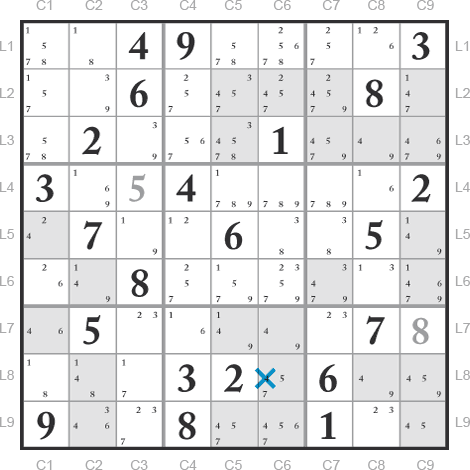
La première chose à faire est d’isoler toutes les occurrences d’un même candidat. C’est ce que nous avons fait dans la grille ci-dessous pour le candidat 4. Toutes les cases grises contiennent un candidat 4. Il faut ensuite choisir une zone sudoku n’ayant que peu d’occurrences de ce même candidat. Nous avons le choix entre le bloc 4 ou la ligne 5.

Partons du bloc 4.
Le principe de la méthode sudoku POM est le suivant : on se positionne dans un cas de figure donné (Pattern, en anglais), c’est-à-dire que l’on va voir, pour chaque candidat 4 du bloc 4, considéré comme bon, ce qu’il entraîne comme modifications dans les autres cases grises.
Le premier cas de figure sera nommé Pattern a : il part du 4 de L6C2. Chaque 4 validé sera aussi noté « a » et chaque 4 invalidé sera noté « – ».
Les deux autres cas de figure partent du 4 de L5C1 et seront nommés Pattern b et Pattern c. De la même manière, un 4 validé sera noté « b » ou « c » selon le cas de figure et chaque 4 invalidé sera noté « – ».

Dans notre exemple, nous aurons donc trois Patterns notés a, b et c.
Une fois ces opérations effectuées, nous superposerons les Patterns :
1 – S’il existe une case ayant les trois lettres, a, b et c, alors on peut affirmer que cette case contient le 4.
2 – S’il existe une case n’ayant que des « – », alors on peut affirmer que cette case n’aura jamais le 4 et on peut donc le supprimer.
Dans notre exemple, nous arriverons à la conclusion de supprimer le 4 de L8C6.
Voici notre raisonnement :

Pattern a Pattern b Pattern c

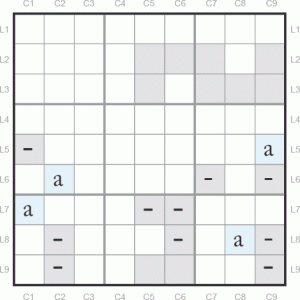
Nous nous intéressons ici aux deux tiers inférieurs de la grille.
 
Dans le premier cas, nous avons présumé que le 4 se situait en L6C2 : nous positionnons « a » dans cette case et nous voyons les conséquences. On trouve alors un 4 en L5C9, L8C8 et L7C1. On positionne des signes « – » en L5C1, L6C79, L7C56, L8C269 et L9C29 puisque le candidat 4 est alors invalidé.
Ceci représente notre premier cas de figure : Pattern a.
 
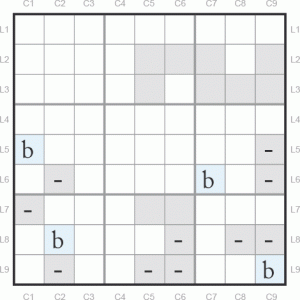
Deuxième cas de figure : le candidat 4 du bloc 4 ne se situe pas dans la case L6C2, il sera donc en L5C1. Cette éventualité fait l’objet de notre Pattern b. Positionnons la lettre « b » dans cette case et examinons-en les conséquences. On met un « – » dans les cases L5C9, L6C2 et L7C1. Il n’y a aucune autre possibilité directe.
Dans le bloc 7, il y a deux possibilités : la case L8C2 et la case L9C2.
Le premier cas (nous mettons un « b » en L8C2) correspondra à la suite de notre Pattern b et le deuxième (nous mettons un « c » en L9C2) à notre Pattern c.
Continuons donc à modeler notre Pattern b en mettant « b » en L9C9 et L6C7 et en positionnant les signes « – » en L9C256, L8C689 et L6C9.
 
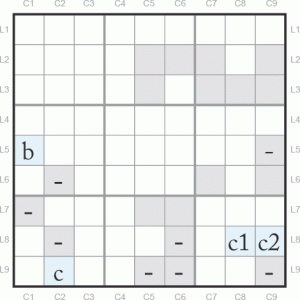
Poursuivons notre chemin avec le Pattern c. On met « – » dans les cases L8C2 et L9C569. Dans le bloc 9, il ne reste que deux possibilités pour le 4 qui sera en L8C8 (c1) ou L8C9 (c2). Sur la ligne 8 donc, on peut mettre un signe « – » dans toutes les autres cases de la ligne et en particulier dans la case L8C6.
Nos trois Patterns étant réalisés, on remarque que quel que soit le choix du départ (4 en L5C1 ou en L6C2), la case L8C6 aura toujours un signe « – ».
On peut donc supprimer le candidat 4 de cette case.